Let the music play

char a;float b,c;main(d){for(;d>2e3*c?c=1,scanf(" %c%f",&a,&c),d=55-a%32*9/5,
b=d>9,d=d%13-a/32*12:1;a=2)++d<24?b*=89/84.:putchar(a=b*d);}

Good news for all International Obfuscated C Code Contest fans -- here's another winning piece from 2013 written by Yusuke Endoh, who is no stranger to the Contest. It is dubbed the Most Tweetable 1-Liner, because is small enough to fit in a tweet (137 characters only), yet can "tweet out a tune", that is, will play some music for your entertainment.

Running the code

The code compiles with some harmless warnings on a modern system. The resulting binary reads musical notes from standard input and synthesises the music to the standard output.

The author advises redirecting the output to /dev/dsp:

% echo "CDEFGABc" | ./endoh3 > /dev/dsp
zsh: permission denied: /dev/dsp
% ls /dev/dsp
ls: cannot access '/dev/dsp': No such file or directory

As you can see, my Linux system (Debian "testing") uses PulseAudio and does not have /dev/dsp anymore. What worked for me is piping the output to aplay:

% echo "CDEFGABc" | ./endoh3 | aplay
Playing raw data 'stdin' : Unsigned 8 bit, Rate 8000 Hz, Mono

If all goes well, you should hear the eight notes, bringing back memories of the dark ages where the only devices in your PC that could emit sounds were the horrible PC-Speaker and a 5.25" floppy disk drive. (Take a look at the author's hints if you can't get it to play on your system.)

Let's move on to the next step -- it's working, so let's take it apart and peek inside!

Cleaning it up

The author has managed to stuff everything in a single for loop -- quite an impressive achievement in minimizing the program, at the cost of readability. To have a better view, let's untangle the code.

#include <stdio.h>

float name2freq(char name) {
    float b;
    int d;

    d = 55 - name % 32 * 9 / 5;
    b = (float)(d > 9);
    d = d % 13 - name / 32 * 12;
    while (++d < 24)
        b *= 89.0 / 84.0;
    return b;
}

int readnote(float *freq, float *len) {
    char name;
    float notelen = 1;

    if (scanf(" %c%f", &name, &notelen) == EOF)
        return 0;
    *freq = name2freq(name);
    *len = notelen;
    return 1;
}

int main() {
    float freq, len;
    while (readnote(&freq, &len))
        for (int d = 24; d <= 1 + 2000 * len; ++d)
            putchar((char)(freq * d));
}

What we see here will not fit in a tweet anymore -- not even after Twitter raised the maximum length from 140 to 280 characters. The code is way more readable because the big for loop is unrolled, and produces exactly the same output as the original program. (I double checked it.)

Now we can see that the code reads notes from standard input with scanf, then writes binary data to the standard output. According to the author, the output data is 8000 Hz, unsigned 8 bit and monophonic -- this is consistent with what aplay shows during playback.

The sound is generated in the main function. There is no surprises here -- we can easily notice that inside the loop, (freq * d) cast to a char will overflow when it goes over 255 -- this is used to generate the sawtooth wave.

The most interesting function here is name2freq. What is b = (float)(d > 9); used for? Why does it divide 89 by 84?

Note frequencies

Let's have a closer look at the name2freq function. It uses a formula to convert the ascii codes of note names into something more useful for generating music. We can have a look at the numbers with this code snippet:

char tmp[] = "CDEFGABcdefgab";
for (char *n = tmp; *n != 0; *n++)
    printf("%c = %f\n", *n, name2freq(*n));

This bit of code shows the function output for the notes, as follows:

The first question is: Why are these numbers so small? The human hearing range is between 20 Hz and 20000 Hz -- if these were real frequencies of the notes, they would be way below. This snippet will help us figure it out:

for (int d = 24; d <= 1 + 2000 * len; ++d)
    putchar((char)(freq * d));

We know the code generates raw sound data with the rate of 8000 Hz -- that is, 8000 of 8-bit samples (bytes) of data for one second of sound. If freq was equal to 1, the loop would output all the bytes from 0 to 255 repeatedly, generating a sawtooth wave with the length of 256 samples. We can calculate frequency of such wave:

$$ F = \frac{8000 \mathrm{Hz}}{256} = 31.25 \mathrm{Hz} $$

Multiplying the loop variable by freq makes the wavelength shorter. Let's see how it goes for C:

$$ F = \frac{8000 \mathrm{Hz}}{ \frac{256}{8.016519} } = \frac{8000 \mathrm{Hz}}{256} \cdot 8.016519 = 31.25 \mathrm{Hz} \cdot 8.016519 = 250.516206 \mathrm{Hz} $$

We can calculate the note frequencies now:

char tmp[] = "CDEFGABcdefgab";
for (char *n = tmp; *n != 0; *n++) {
    float f = name2freq(*n);
    printf("%c = %f = %f Hz\n", *n, f, 31.25 * f);
}

We can see these values are slightly out of tune -- according to the ISO 16 standard, A should have the frequency of 440 Hz. Don't worry, you will still be able to recognize the music.

Alphabet of music

Let's go one step further and pass the whole alphabet to the function letter by letter!

for (char n = 'A'; n <= 'z'; n++) {
    float f = name2freq(n);
    printf("%f\t%c\t%f Hz\n", f, n, 31.25 * f);
}

Here is the result, nicely wrapped in a table sorted by the frequency.

Looking at this table, we can draw some interesting conclusions.

First of all, the experiment shows us what the expression b = (float)(d > 9) is used for. It evaluates to 0 for capital and small letter Z and some other non-alphabetic characters; this is how the code handle rests in the notes (zero frequency -- no sound at all). We also learn how to make the code emit half-tones, as it doesn't handle sharps and flats -- you just need to find a letter that will give a frequency somewhere between your notes! For C# (the note, not the language), you can use either K, R or Y.

Twelve roots

Our next riddle to solve here is the magic 89.0 / 84.0 number. The result of this division is about 1.059524, and it is used to calculate the note frequencies by repeated multiplications. After some digging on the world's favourite encyclopedia I found that this number is a quite good approximation of the twelfth root of 2, \( \sqrt[12]{2} \), and is the smallest interval in the twelve-tone equal temperament scale. What does it all mean? We will learn more about it in just a moment.

The obvious question here is: why not just use pow(2, 1.0/12.0)? The author decided against it so that he won't have to include math.h, which would make the code longer - most probably it will no longer fit in a tweet. Also, the code won't be a one-liner anymore, as includes in C need to go on separate lines. But how do you come up with numbers like these?

Herr Stern and Monsieur Brocot

Mr Stern was a German mathematician; Mr Brocot was a clockmaker from France. They both independently discovered a structure called a Stern-Brocot tree; an infinite binary tree containing all positive rational numbers, with values ordered from left to right as in a binary search tree. One of its uses is to approximate floating-point numbers to arbitrary precision.

(Once you wrap your head around the fact that in computer science, trees have roots at the top and grow downwards, things start to make more sense.)

The idea here is pretty simple. You start with two fractions, \( \frac{0}{1} \) representing zero and \( \frac{1}{0} \) for infinity, and insert a mediant between them. A mediant of two fractions, \( \frac{a}{b} \) and \( \frac{c}{d} \), is defined as a fraction where the numerator is the sum of numerators, and the denominator is the sum of denominators, so: \( \frac{a+b}{c+d} \). An important property of the mediant is the mediant inequality:

$$ \frac{a}{b} < \frac{a+b}{c+d} < \frac{c}{d} $$

For \( \frac{0}{1} \) and \( \frac{1}{0} \) , the mediant is going to be \( \frac{1}{1} \). Then, in the next step, insert mediants between adjacent fractions.

$$ Step\ 1: \frac{0}{1} , \frac{1}{1} , \frac{1}{0} $$ $$ Step\ 2: \frac{0}{1} , \frac{1}{2}, \frac{1}{1}, \frac{2}{1}, \frac{1}{0} $$

The tree can be expanded indefinitely.

Aaron Rotenberg made a nice picture of the tree for Wikipedia, let's have a look at it:

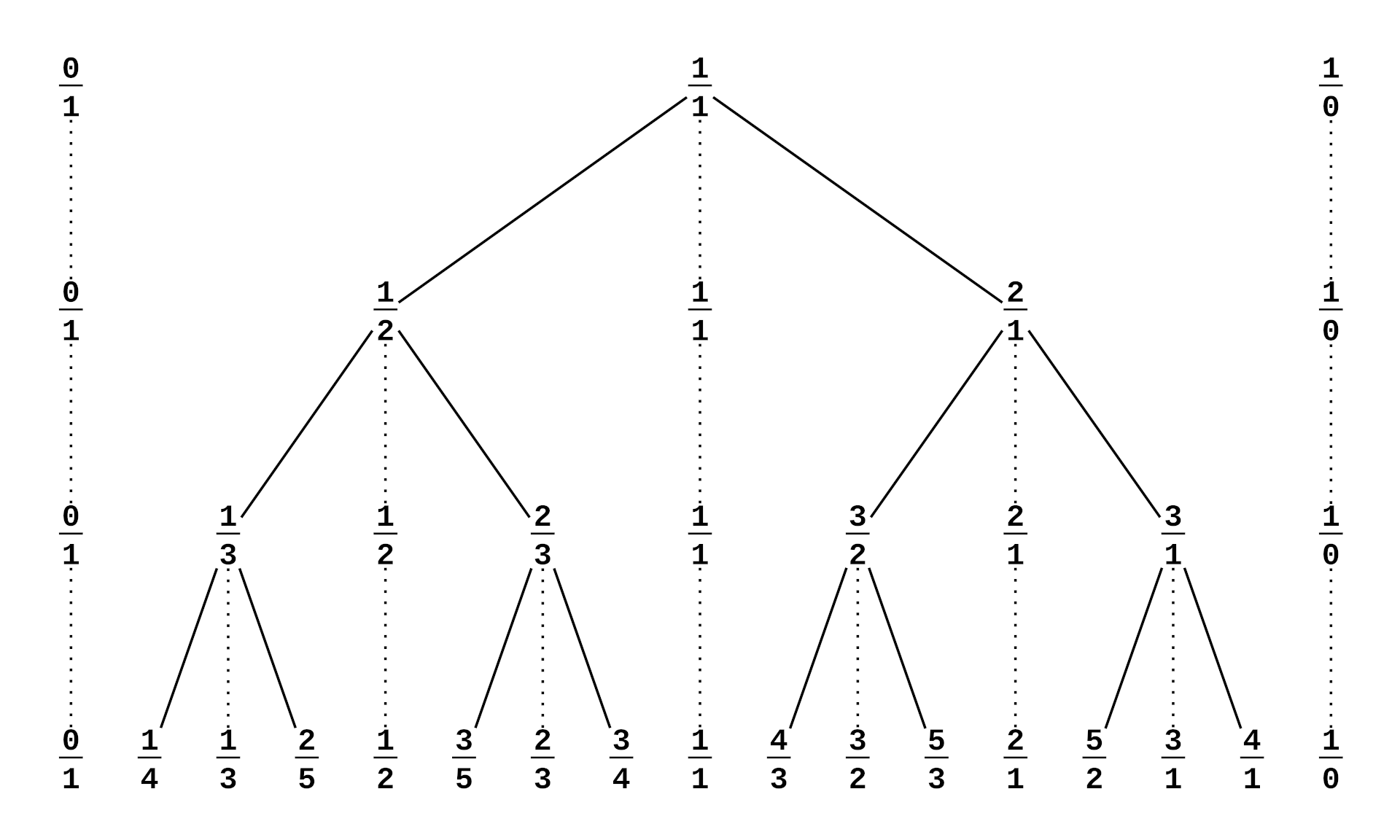
To approximate a number, we need to do a series of comparisons. We start with 1 - if the number is smaller, go left; if it's larger, go right. Keep going down the tree until you found the number (or one that's close enough).

Let's calculate

package main

import (
	"fmt"
	"math"
)

type frac struct {
	num, denom int
}

func (f *frac) val() float64 {
	return float64(f.num) / float64(f.denom)
}

func between(a, b frac) frac {
	return frac{a.num + b.num, a.denom + b.denom}
}

func eq(a, b, eps float64) bool {
	return math.Abs(a-b) <= eps
}

func approx(num, eps float64) frac {
	left := frac{0, 1}
	right := frac{1, 0}
	s := between(left, right)

	for !eq(num, s.val(), eps) {
		if num < s.val() {
			s = between(left, s)
		} else {
			s = between(s, right)
		}
	}
	return s
}

func main() {
	const eps float64 = 0.0001
	n := math.Pow(2, 1/12.)
	s := approx(n, eps)
	fmt.Printf("%f is about %d/%d\n", n, s.num, s.denom)
}

"That ain't no Hank Williams song!", some might say looking at the code above. I have been experimenting with Go lately and wrote this tiny program to calculate the approximations. Even if you don't know Go at all, the code should be quite straightforward. (Hint: the for loop is actually a while.)

% go run approx.go
1.059463 is about 89/84

We just found the exact same fraction that we have seen in the original code. Just for the fun of it, let's approximate Pi:

3.141593 is about 333/106

Looks pretty close to the real thing, doesn't it?

Sound waves

How do you actually make sounds? The whole idea is to generate waves with the right frequencies, to make the speaker's membranes move and produce sound. We know how does the code generate waves, but how do we know which frequencies are right?

It turns out, we can begin our scale with any frequency, as long as we keep the right distances between notes. Earlier we mentioned the twelve roots and equal temperament scale -- let's talk a bit more about it now.

A twelve tone equal temperament scale is a logarithmic scale, with a ratio equal to the twelfth root of 2. It is the most common tuning system since the 18th century.

$$ \sqrt[12]{2} \approx 1.059463 $$

To calculate a given note frequency from a base frequency, we can use the following formula:

$$ P_n = P_a \left( \sqrt[12]{2} \right)^{(n-a)} $$

Now everyone needs to agree on the base frequency and nothing goes out of tune.

Such a basic frequency is 440Hz for A4, the 49th key on the piano. So, C4 being a 40th key would have a frequency of:

$$ P(C_4) = P_{40} = 440 \mathrm{Hz} \left( \sqrt[12]{2} \right)^{(40-49)} \approx 440 \mathrm{Hz} \cdot 1.059463 ^{-9} \approx 261.625775 \mathrm{Hz} $$

Like I said before, we are slightly out of tune, with our C equal to 250.516206 Hz. This does not pose a problem, because we are not playing with other instruments.

Conclusion

To understand the magic in 137 bytes of code, we went through music theory, a clever approximation algorithm, a great way to decode music note names to their frequencies, and sound wave generation. What a ride!

Exercise for the reader: Byte the music

main(t){
    for(t=0;;t++)putchar(
        (t>>6|t|t>>(t>>16))*10+((t>>11)&7)
);}

This little piece of code (or "bytebeat") written by viznut uses the same technique to generate music procedurally. The output, when treated as audio, sounds a lot like chip tune music from retro video games. How is it possible for just one short formula to contain this much of music?

Further reading

• Why 12 notes to the octave?
• How Music Works